រូបមន្តសម្រាប់គណនាផ្ទៃនៃចតុកោណកែង

ដើម្បីគណនាផ្ទៃដីនៃចតុកោណកែង បន្ថែមពីលើការគុណប្រវែងដោយទទឹង វាក៏អាចគណនាបានដែរ នៅពេលដែលដឹងផ្នែកម្ខាង និងបន្ថែមអង្កត់ទ្រូង ឬបរិវេណ។

ទិដ្ឋភាពរហ័ស៖

• តើចតុកោណកែងជាអ្វី?
• រូបមន្តសម្រាប់គណនាផ្ទៃនៃចតុកោណកែង
• រូបមន្ត​សម្រាប់​គណនា​ផ្ទៃ​នៃ​ចតុកោណ​ពេល​ដឹង 1 ចំហៀង និង​អង្កត់ទ្រូង
• រូបមន្តសម្រាប់គណនាផ្ទៃដីនៃចតុកោណកែងនៅពេលដឹងបរិវេណ
• សញ្ញាសម្គាល់ចតុកោណកែង?
• តើ​ចតុកោណ​ជា​ប្រលេឡូក្រាម​ឬ?
• តើ​ចតុកោណកែង​ជា​ isosceles trapezoid?

តើចតុកោណកែងជាអ្វី?

យោងតាមមេរៀនទី ១៣ គណិតវិទ្យាទី ៨ (វគ្គ ១) នៃសៀវភៅសិក្សា "ការតភ្ជាប់ចំណេះដឹងជាមួយជីវិត" ដោយគ្រឹះស្ថានបោះពុម្ពផ្សាយ អប់រំ វៀតណាម និយមន័យនៃចតុកោណកែងគឺជាចតុកោណកែងដែលមានមុំខាងស្តាំចំនួន ៤ ។

លក្ខណសម្បត្តិនៃចតុកោណកែងគឺវាមាន 2 ជ្រុងទល់មុខប៉ារ៉ាឡែល 2 ជ្រុងផ្ទុយគ្នាស្មើគ្នា 2 មុំទល់មុខស្មើគ្នា 2 អង្កត់ទ្រូងស្មើគ្នា និងប្រសព្វនៅចំនុចកណ្តាលនៃបន្ទាត់នីមួយៗ។

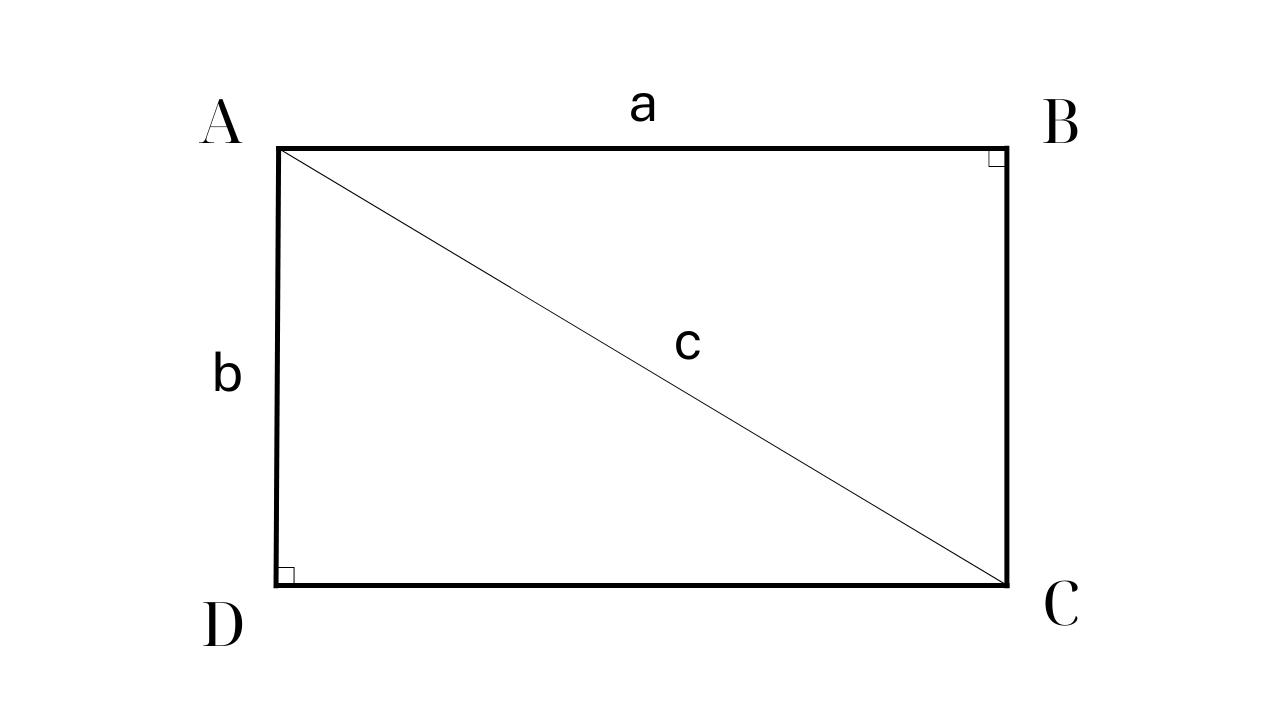
រូបមន្តសម្រាប់គណនាផ្ទៃនៃចតុកោណកែង

នៅក្នុងមេរៀនទី 52 សៀវភៅគណិតវិទ្យាទី 3 (ភាគ 2) នៃស៊េរីសៀវភៅសិក្សា "ការតភ្ជាប់ចំណេះដឹងជាមួយជីវិត" ដោយគ្រឹះស្ថានបោះពុម្ពអប់រំវៀតណាម រូបមន្តសម្រាប់គណនាផ្ទៃដីនៃចតុកោណគឺប្រវែងគុណនឹងទទឹង (ឯកតារង្វាស់ដូចគ្នា)។

S = axb

នៅទីនោះ៖

S: តំបន់​នៃ​ចតុកោណ

ក៖ ប្រវែងចតុកោណ

b: ទទឹងនៃចតុកោណកែង

ឧទាហរណ៍៖ បន្ទះឈើរាងចតុកោណមានទទឹង 5cm និងប្រវែង 15cm។ គណនាផ្ទៃដីនៃបន្ទះឈើនោះ។

ចំលើយ៖ ផ្ទៃក្តារ៖ S = 5 x 15 = 75 (cm ² )

រូបមន្ត​សម្រាប់​គណនា​ផ្ទៃ​នៃ​ចតុកោណ​ពេល​ដឹង 1 ចំហៀង និង​អង្កត់ទ្រូង

ដើម្បីគណនាផ្ទៃដីនៃចតុកោណកែង នៅពេលដឹងពីអង្កត់ទ្រូង និងផ្នែកម្ខាង វាចាំបាច់ក្នុងការបញ្ចូលគ្នានូវទ្រឹស្តីបទពីតាហ្គោរ ជាមួយនឹងរូបមន្តផ្ទៃមូលដ្ឋាន។

ជំហានទី 1: អនុវត្តទ្រឹស្តីបទពីថាហ្គោរក្នុងត្រីកោណកែងដើម្បីគណនាប្រវែងនៃផ្នែកដែលនៅសល់។

ជំហានទី 2: អនុវត្តរូបមន្តដើម្បីគណនាផ្ទៃនៃចតុកោណកែងមួយ: S = axb

ឧទាហរណ៍៖ ចតុកោណកែង ABCD មាន AD = 60cm អង្កត់ទ្រូង AC គឺ 100cm។ គណនាផ្ទៃ ABCD ។

ចម្លើយ៖

ជំហានទី 1: ស្វែងរកផ្នែកដែលនៅសល់នៃចតុកោណកែង ABCD ដោយប្រើទ្រឹស្តីបទពីថាហ្គោរនៅក្នុងត្រីកោណកែងមួយ។

ដូច្នោះ៖ AC ² = AB ² + AD ² => AB ² = AC ² - AD ² = 10000 - 3600 = 6400 => AB = 80 (សង់ទីម៉ែត្រ)

ជំហានទី 2៖ ផ្ទៃដី ABCD = AB x AD = 60 x 80 = 4800 (cm ² )

រូបមន្តសម្រាប់គណនាផ្ទៃដីនៃចតុកោណកែងនៅពេលដឹងបរិវេណ

ដើម្បីគណនាផ្ទៃដីនៃចតុកោណកែង នៅពេលដឹងពីបរិវេណ អ្នកត្រូវតែផ្សំរូបមន្តបរិវេណ និងរូបមន្តផ្ទៃមូលដ្ឋាន។

ជំហានទី 1: ពីរូបមន្តសម្រាប់គណនាបរិវេណនៃចតុកោណគឺ P = (a + b) x 2 ជាមួយ P គឺជាបរិវេណ a គឺជាប្រវែង b គឺជាទទឹងនៃចតុកោណយើងមាន a = (P/2) - b ឬ b = (P/2) - a

ជំហានទី 2: បន្ទាប់ពីរកឃើញ a ឬ b សូមអនុវត្តរូបមន្តដើម្បីគណនាផ្ទៃនៃចតុកោណកែង៖ S = axb

សញ្ញាសម្គាល់ចតុកោណកែង?

យោងតាមមេរៀនទី 13 គណិតវិទ្យាទី 8 (វគ្គ 1) ស៊េរីសៀវភៅសិក្សា "ការភ្ជាប់ចំណេះដឹងជាមួយជីវិត" ដោយគ្រឹះស្ថានបោះពុម្ពផ្សាយអប់រំវៀតណាម សញ្ញាសម្គាល់ចតុកោណកែងគឺ៖

- ចតុកោណកែងមាន 3 មុំខាងស្តាំ (ផ្អែកលើនិយមន័យ)

- Parallelogram មាន 1 មុំខាងស្តាំ

- ប្រលេឡូក្រាមមានអង្កត់ទ្រូងពីរស្មើគ្នា។

- isosceles trapezoid មានមុំខាងស្តាំមួយ។

តើ​ចតុកោណ​ជា​ប្រលេឡូក្រាម​ឬ?

យោងតាមមេរៀនទី 13 គណិតវិទ្យាទី 8 (វគ្គ 1) ស៊េរីសៀវភៅសិក្សា "ការតភ្ជាប់ចំណេះដឹងជាមួយជីវិត" ដោយគ្រឹះស្ថានបោះពុម្ពផ្សាយអប់រំវៀតណាម ចតុកោណកែងមានលក្ខណៈសម្បត្តិទាំងអស់នៃប្រលេឡូក្រាម។ ដូច្នេះ ចតុកោណកែង គឺជាប្រលេឡូក្រាមពិសេស។

តើ​ចតុកោណកែង​ជា​ isosceles trapezoid?

មេរៀនទី១៣ គណិតវិទ្យាទី៨ (វគ្គ១) សៀវភៅសិក្សា "ការភ្ជាប់ចំណេះដឹងជាមួយជីវិត" ដោយគ្រឹះស្ថានបោះពុម្ពផ្សាយអប់រំវៀតណាម ចតុកោណកែងមានលក្ខណៈសម្បត្តិទាំងអស់នៃរាងចតុកោណកែង។ ដូច្នេះចតុកោណកែងគឺជាទម្រង់ពិសេសនៃ isosceles trapezoid ។

(សំយោគ)

ប្រភព៖ https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html