평면 기하학에서 원은 고정된 점(중심이라고 함)으로부터 반지름이라고 하는 특정 거리를 두고 같은 거리에 있는 모든 점의 집합입니다.
원의 반지름은 0보다 큰 양수여야 합니다.
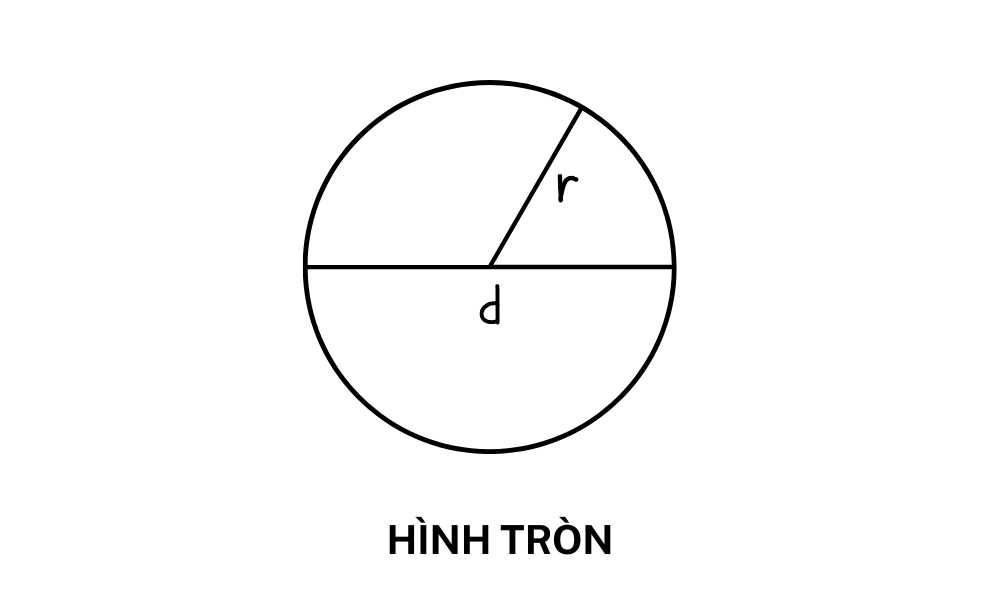
원과 원은 두 가지 다른 개념입니다.
원은 원 안과 위에 있는 모든 점의 집합입니다. 다시 말해, 원은 단면이므로 넓이를 갖습니다.
원은 평면에서 주어진 점(중심이라고 함)으로부터 거리가 같은 모든 점의 집합입니다. 닫힌 곡선(윤곽선, 경계 등)은 면적이 없습니다.
원의 넓이는 반지름의 제곱에 파이를 곱하여 계산합니다.
| S = rxrxnbsp;π = r 2 x π |
거기에는:
S: 원의 면적
r: 원의 반지름 - 원의 중심에서 원 위의 임의의 점까지의 거리입니다.
π(파이): 파이는 수학 상수로, 약 3.14159와 같습니다.
수학과 기하학에서 지름은 원의 중심을 지나 원 위의 두 점을 연결하는 선분입니다. 지름은 원에서 가장 긴 선분으로, 원을 두 개의 동일한 반쪽으로 나누고 길이는 반지름의 두 배입니다.
지름 데이터만 있는 문제의 경우, 지름의 1/2 제곱에 파이를 곱하여 원의 면적을 계산하는 공식을 사용하세요.
| S = (d/2) 2 x π |
거기에는:
S: 원의 면적
d: 원의 지름의 길이
π(파이): 파이는 수학 상수로, 약 3.14159와 같습니다.
원의 둘레는 원을 둘러싼 경로의 길이입니다. 둘레(C)를 계산하는 공식은 C = π x d (여기서 d는 지름) 또는 C = 2 x r x π (여기서 r은 반지름)입니다.
원주율 데이터만 있는 문제의 경우, 원의 면적을 계산하는 방법은 두 가지가 있습니다.
방법 1: 일반 공식 사용:
| S = r 2 x π |
- 1단계: 원주(C)에서 반지름(r)을 구합니다.
원의 둘레는 C = 2 xrx π이므로 r =C/(2π)입니다.
- 2단계: 원의 면적을 계산하는 공식 적용
원의 면적은 S = r 2 x π입니다. 1단계에서 구한 새로운 r을 대입하면 S = (C/2π)² x π가 됩니다.
단순화하면 최종 공식은 S = (C) 2 /4π가 됩니다.
방법 2: 원의 면적을 계산하기 위해 원주율의 제곱을 4 곱하기 파이로 나누어 단순화된 공식을 적용합니다.
| S = (C) 2 / 4π |
거기에는:
S: 원의 면적
C: 원의 둘레
π(파이): 파이는 수학 상수로, 약 3.14159와 같습니다.
원의 면적은 면적 단위(mm2, dm2, cm2, m2...)를 사용해야 합니다.
원의 반지름, 지름, 둘레는 길이 단위(mm, dm, cm, m...)를 사용해야 합니다.
출처: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-tron-la-gi-2441504.html







![[사진] 중앙당기관 당대표자대회 제1차 대회 폐막](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/24/b419f67738854f85bad6dbefa40f3040)



















![[사진] Nhan Dan 신문 편집장 Le Quoc Minh이 Pasaxon 신문의 실무 대표단을 접견했습니다.](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/23/da79369d8d2849318c3fe8e792f4ce16)


































![[사진] 중앙당기관 당대표자대회 제1차 대회 성대히 개막](https://vphoto.vietnam.vn/thumb/402x226/vietnam/resource/IMAGE/2025/9/24/82a89e250d4d43cbb6fcb312f21c5dd4)




























댓글 (0)