円とは何ですか?
円とは、平面上に位置し、ある点(中心)から等距離で一定の距離(半径 - r)にあるすべての点の集合です。円の中心は、円の中心にある固定点です。直径(d):円の中心を通り、円上の2点を結ぶ線分で、d=2rに等しくなります。
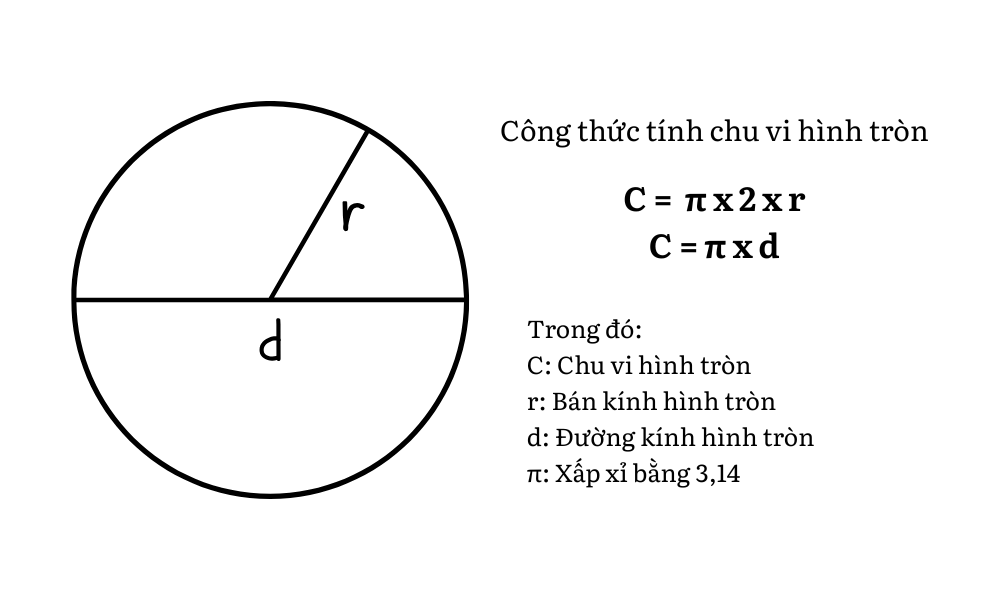
半径がわかっている場合の円周の計算式
教科書「知識と人生をつなぐ」の数学 5、第 1 巻、レッスン 27 によると、円の円周を計算するには、3.14 に 2 を掛け、さらに半径を掛けます。
| C = π × 2 × r |
そこには:
Cは円周です
dは円の直径です
rは円の半径です
πは定数(3.14に相当)
例:半径 5cm の円の円周を計算します。
答え:円周 C = 3.14 x 2 xr = 3.14 x 2 x 5 = 31.4 (cm)
直径がわかっている場合の円周の計算式
直径は半径の 2 倍なので、直径がわかっている場合に円周を計算するには、3.14 に 2 を掛け、さらに半径を掛けます。
| C = π × d |
例:直径 6dm の円の円周を計算します。
答え: 円周 C = 3.14 x d = 3.14 x 6 = 18.84 (dm)
円周を計算するのにどのくらいの円周率を使用できますか?
教科書シリーズ「知識と生活をつなぐ」の「数学 5」の小数の四捨五入のセクションでは、数値 π\pi が、小数点以下の桁数が多い特殊な数値として紹介されており、「3.141592...」のように、10 分の 1 と 100 分の 1 に四捨五入する必要があります。
6 年生の数学 (ワークブック - 新しいプログラム) によると、教科書では、π\piπ はアルキメデスの定数であり、円周と直径の比に等しく、おおよその値は「3.141592653589793…」であると説明されており、この数値を四捨五入する練習問題も含まれています。
したがって、レッスンの要件に応じて、適切な丸められた円周率の値を選択できます。
円の寸法を示すのに C、S、r、d の文字が使用されるのはなぜですか?
C は「円周」、S は「表面積」、r は「半径」、d は「直径」を表します。
これらの文字を使用すると、数学表記が短く、覚えやすく、 広く受け入れられるようになります。
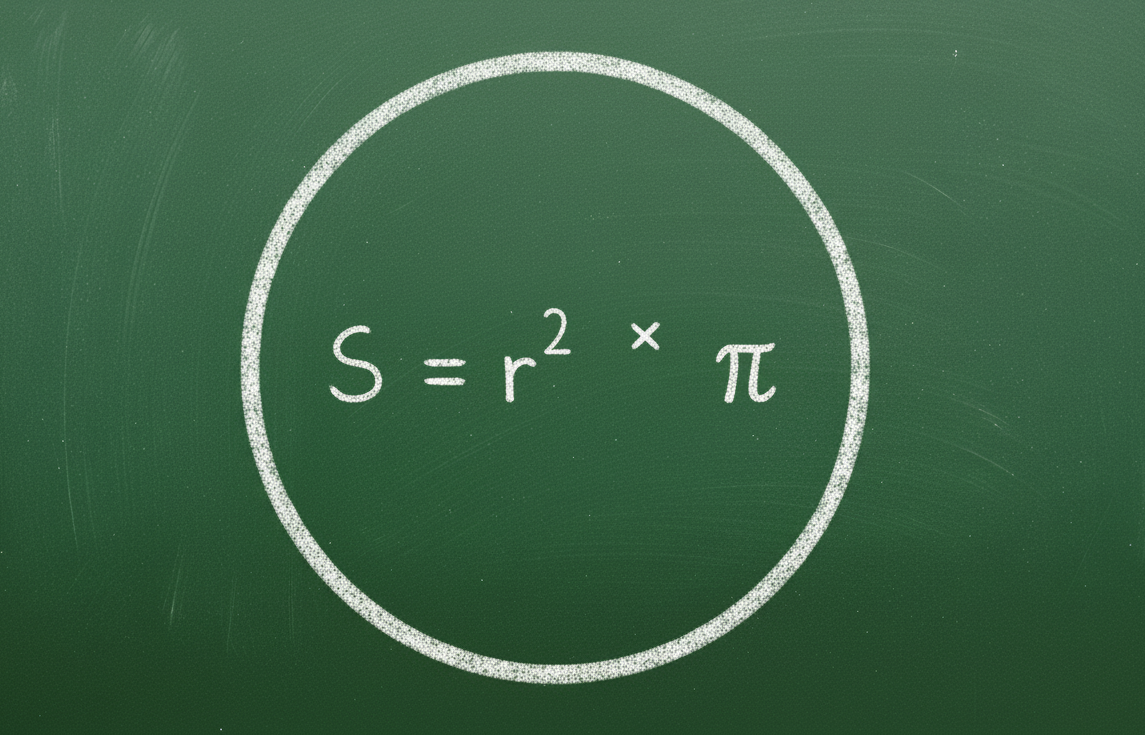
出典: https://vietnamnet.vn/cong-thuc-tinh-chu-vi-hinh-tron-2445269.html



![[写真] フート省党委員会第1回大会(任期2025~2030年)](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/30/1507da06216649bba8a1ce6251816820)
![[写真] ト・ラム事務総長がベトナム駐在米国大使マーク・ナッパー氏を接見](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/29/c8fd0761aa184da7814aee57d87c49b3)
![[写真] 2025~2030年任期の第12回軍事党大会が厳粛に開幕](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/30/2cd383b3130d41a1a4b5ace0d5eb989d)



























































































コメント (0)