Wie lautet die Formel zur Berechnung der Fläche eines Kreises?

Was ist ein Kreis?

In der ebenen Geometrie ist ein Kreis die Menge aller Punkte, die von einem festen Punkt (dem Mittelpunkt) mit einem bestimmten Abstand, dem Radius, gleich weit entfernt sind.

Der Radius des Kreises muss eine positive Zahl größer als 0 sein.

Wie unterscheidet sich ein Kreis von einem Kreis?

Kreis und Kreis sind zwei verschiedene Konzepte.

Ein Kreis ist die Menge aller Punkte, die innerhalb und auf dem Kreis liegen. Mit anderen Worten: Ein Kreis ist ein Querschnitt und hat daher eine Fläche.

Ein Kreis ist der Ort aller Punkte auf einer Ebene, die von einem bestimmten Punkt (dem sogenannten Mittelpunkt) gleich weit entfernt sind – eine geschlossene Kurve (z. B. eine Kontur oder Grenze) hat keine Fläche.

Formel zur Berechnung der Fläche eines Kreises

Die Fläche eines Kreises wird berechnet, indem das Quadrat des Radius mit Pi multipliziert wird.

S = rxrxnbsp;π = r ² x π

Darin:

S: Fläche eines Kreises

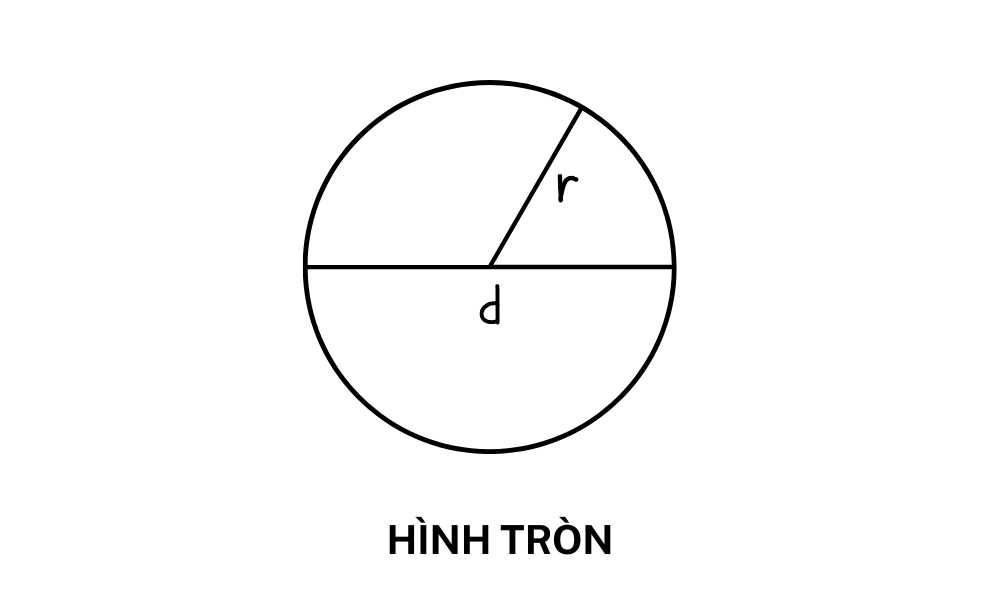
r: Radius eines Kreises – ist der Abstand vom Mittelpunkt des Kreises zu einem beliebigen Punkt auf dem Kreis.

π (Pi): Die Zahl Pi ist eine mathematische Konstante, die ungefähr 3,14159 entspricht

So berechnen Sie die Fläche eines Kreises, wenn Sie den Durchmesser kennen

In der Mathematik und Geometrie ist ein Durchmesser ein Liniensegment, das durch den Mittelpunkt eines Kreises verläuft und zwei beliebige Punkte auf dem Kreis verbindet. Der Durchmesser ist das längste Liniensegment eines Kreises. Er teilt den Kreis in zwei gleiche Hälften und hat eine Länge, die dem doppelten Radius entspricht.

Verwenden Sie bei Problemen, bei denen nur der Durchmesser angegeben wird, die Formel zur Berechnung der Fläche eines Kreises durch das Quadrat von ½ des Durchmessers multipliziert mit Pi.

S = (d/2) ² x π

Darin:

S: Fläche eines Kreises

d: Länge des Kreisdurchmessers

π (Pi): Die Zahl Pi ist eine mathematische Konstante, die ungefähr 3,14159 entspricht

So berechnen Sie die Fläche eines Kreises, wenn Sie den Umfang kennen

Der Umfang eines Kreises ist die Länge des Weges um den Kreis. Die Formel zur Berechnung des Umfangs (C) lautet C = π xd (wobei d der Durchmesser ist) oder C = 2 xrx π (wobei r der Radius ist).

Bei Problemen mit ausschließlich Umfangsdaten gibt es zwei Möglichkeiten, die Fläche eines Kreises zu berechnen.

Methode 1: Mit der allgemeinen Formel:

S = r ² x π

- Schritt 1: Ermitteln Sie den Radius (r) aus dem Umfang (C).

Der Umfang eines Kreises beträgt C = 2 xrx π, also r =C/(2π)

- Schritt 2: Wenden Sie die Formel an, um die Fläche eines Kreises zu berechnen

Die Fläche eines Kreises beträgt S = r ² x π. Ersetzen Sie das in Schritt 1 ermittelte neue r, um zu erhalten: S = (C/2π)² x π

Nach der Vereinfachung erhalten wir die endgültige Formel: S = (C) ² /4π.

Methode 2: Wenden Sie die vereinfachte Formel an, um die Fläche eines Kreises zu berechnen, indem Sie das Quadrat des Umfangs durch 4 mal Pi teilen:

S = (C) ² / 4π

Darin:

S: Fläche eines Kreises

C: Umfang eines Kreises

π (Pi): Die Zahl Pi ist eine mathematische Konstante und entspricht ungefähr 3,14159.

Hinweise zur Berechnung der Kreisfläche

Die Fläche eines Kreises muss in Flächeneinheiten (mm2, dm2, cm2, m2...) angegeben werden.

Radius, Durchmesser und Kreisumfang müssen Längeneinheiten (mm, dm, cm, m...) verwenden.

Quelle: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-tron-la-gi-2441504.html