រូបមន្តលម្អិតសម្រាប់ការគណនាតំបន់នៃ trapezoids

ទិដ្ឋភាពរហ័ស៖

តើអ្វីជា trapezoid?
ការបែងចែកប្រភេទនៃ trapezoids
រូបមន្តមូលដ្ឋានសម្រាប់ការគណនាផ្ទៃនៃ trapezoid មួយ។
តើ trapezoids និង isosceles trapezoids មានរូបមន្តសម្រាប់គណនាតំបន់ជាក់លាក់ទេ?
ព័ត៌មានជំនួយសម្រាប់ការគណនាតំបន់នៃ trapezoid មួយ។

តើអ្វីជា trapezoid?

យោងតាមសៀវភៅសិក្សា ការតភ្ជាប់ចំណេះដឹងជាមួយជីវិត គណិតវិទ្យាទី៥ ភាគ១ មេរៀនទី២៦ រាងចតុកោណក្នុងធរណីមាត្រនៃយន្តហោះ គឺជារាងចតុកោណរាងបួនជ្រុងដែលមានជ្រុងពីរផ្ទុយគ្នាស្របគ្នា។

ការបែងចែកប្រភេទនៃ trapezoids

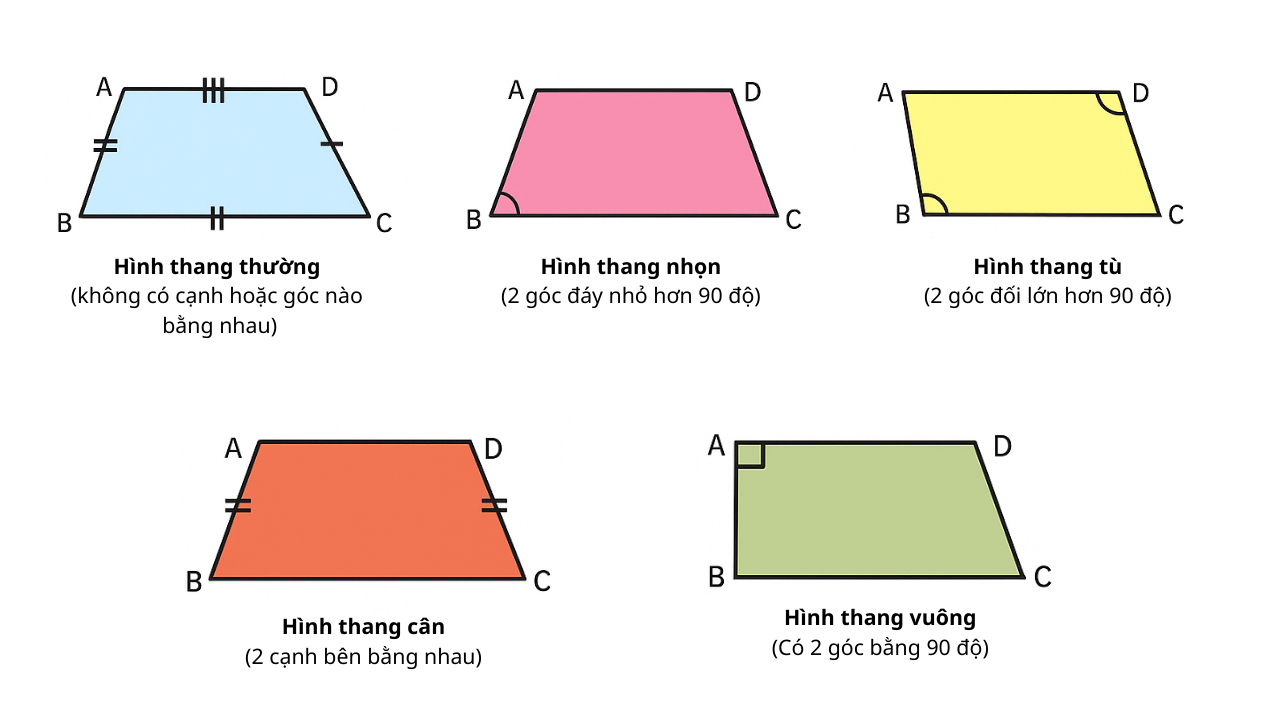
Trapezoids អាចត្រូវបានសម្គាល់ដោយមុំឬលក្ខណៈវិនិច្ឆ័យចំហៀង។

បែងចែកតាមមុំ	បែងចែកដោយគែម
trapezoid ខាងស្តាំ (trapezoid មាន 1 ចំហៀងកាត់កែងទៅ 2 មូលដ្ឋាន)	រាងចតុកោណកែងធម្មតា (មិនមានជ្រុងស្មើគ្នា ឬមុំទេ មានតែ 1 គូនៃភាគីផ្ទុយស្របគ្នា)
រាងចតុកោណស្រួចស្រាវ (រាងចតុកោណដែលមានមុំគោល 2 តិចជាង 90 ដឺក្រេ)	isosceles trapezoid ( trapezoid មាន 2 មុំស្មើគ្នានៅជាប់នឹងមូលដ្ឋានមួយ 2 ជ្រុងស្មើគ្នា 2 អង្កត់ទ្រូងស្មើគ្នាអាចត្រូវបានចារឹកក្នុងរង្វង់មួយ)
Obtuse trapezoid (trapezoid មាន 2 មុំទល់មុខគ្នាធំជាង 90 ដឺក្រេ)

រូបមន្តមូលដ្ឋានសម្រាប់ការគណនាផ្ទៃនៃ trapezoid មួយ។

យោងតាមសៀវភៅសិក្សា ការភ្ជាប់ចំនេះដឹងជាមួយជីវិត គណិតវិទ្យាទី៥ ភាគ១ មេរៀនទី២៦ ផ្ទៃនៃត្រីកោណមាត្រស្មើនឹងប្រវែងសរុបនៃគោល ២ គុណនឹងកំពស់ (ឯកតារង្វាស់ដូចគ្នា) បន្ទាប់មកចែកនឹង ២។

S = ½ [(a+b) xh]

នៅទីនោះ៖

S: តំបន់នៃ trapezoid

a និង b គឺជាប្រវែងនៃមូលដ្ឋានទាំងពីរ

h គឺជាកម្ពស់

ឧទាហរណ៍៖ គណនាផ្ទៃរាងចតុកោណដោយដឹងថា៖ ប្រវែងជើងទាំង២មាន៤សង់ទីម៉ែត្រនិង៦សង់ទីម៉ែត្ររៀងៗខ្លួន កម្ពស់៣សង់ទីម៉ែត្រ។

ចំលើយ៖ S = ½ [(4+6) x 3] = 15 cm ^២

តើ trapezoids និង isosceles trapezoids មានរូបមន្តសម្រាប់គណនាតំបន់ជាក់លាក់ទេ?

ទេ ទោះបីជាពួកវាជា 2 trapezoids ពិសេសក៏ដោយ វាមានរូបមន្តតែមួយគត់ដើម្បីគណនា trapezoid មួយ។

ព័ត៌មានជំនួយសម្រាប់ការគណនាតំបន់នៃ trapezoid មួយ។

ចំពោះបញ្ហាដែលមិនមានទិន្នន័យគ្រប់គ្រាន់លើប្រវែងនៃមូលដ្ឋាន 2 និងកម្ពស់វាមិនអាចទៅរួចទេក្នុងការគណនាតំបន់នៃ trapezoid នេះ។

ប្រវែង និងផ្ទៃត្រូវតែបំប្លែងទៅជាឯកតាដូចគ្នាមុននឹងគណនា។