クイックビュー:
  • 円とは何ですか?
  • 円と円の違いは何でしょうか?
  • 円の面積を計算する公式
  • 直径がわかっている場合の円の面積の計算方法
  • 円周がわかっている場合の円の面積の計算方法
  • 円の面積を計算する際の注意点
円とは何ですか?

平面幾何学では、円は、固定された点 (中心と呼ばれる) から半径と呼ばれる指定された距離だけ等距離にあるすべての点の集合です。

円の半径は 0 より大きい正の数でなければなりません。

円の面積.png
円と円の違いは何でしょうか?

円と円は2つの異なる概念です。

円は、円の内部と円上のすべての点の集合です。言い換えれば、円は断面であり、したがって面積を持ちます。

円は、特定の点（中心と呼ばれる）から等距離にある平面上のすべての点の軌跡です。閉じた曲線（輪郭、境界など）には面積がありません。

円の面積を計算する公式

円の面積は、半径の2乗に円周率を掛けて計算します。

S = rxrxnbsp;π = r 2 x π

そこには：

S: 円の面積

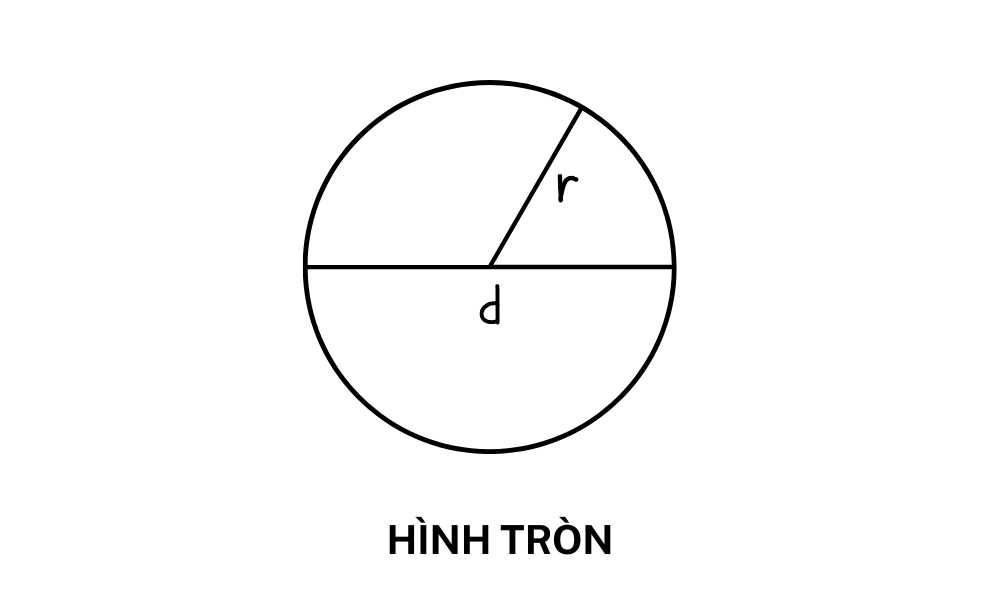
r: 円の半径 - 円の中心から円上の任意の点までの距離です。

π（円周率）：円周率は数学定数で、およそ3.14159に等しい。

直径がわかっている場合の円の面積の計算方法

数学と幾何学において、直径とは円の中心を通り、円上の任意の2点を結ぶ線分のことです。直径は円を2等分する最も長い線分であり、その長さは半径の2倍です。

直径データのみの問題の場合は、直径の1/2の2乗に円周率を掛けて円の面積を計算する公式を使用します。

S = (d/2) 2 × π

そこには：

S: 円の面積

d: 円の直径の長さ

π（円周率）：円周率は数学定数で、およそ3.14159に等しい。

円周がわかっている場合の円の面積の計算方法

円周とは、円周の長さです。円周（C）の計算式は、C = π x d（dは直径）またはC = 2 x rx π（rは半径）です。

円周データのみの問題の場合、円の面積を計算する方法は2つあります。

方法1: 一般的な式を使用する:

S = r 2 × π

- ステップ1: 円周(C)から半径(r)を求める

円周はC = 2 xrx πなので、r =C/(2π)

- ステップ2：円の面積を計算するための公式を適用する

円の面積はS = r 2 x πです。ステップ1で求めた新しいrを代入すると、S = (C/2π)² x πとなります。

簡略化すると、最終式は S = (C) 2 /4π になります。

方法2：円周の2乗を円周率の4倍で割って、簡略化された公式を適用して円の面積を計算します。

S = (C) 2 / 4π

そこには：

S: 円の面積

C: 円周

π (パイ): 円周率は数学定数であり、およそ 3.14159 に等しくなります。

円の面積を計算する際の注意点

円の面積には面積単位（mm2、dm2、cm2、m2など）を使用する必要があります。

円の半径、直径、円周には長さの単位 (mm、dm、cm、m など) を使用する必要があります。

出典: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-tron-la-gi-2441504.html