What is a derivative? Detailed derivative formulas

In addition to all the derivative formulas of common functions, trigonometric derivatives, derivatives of exponential and logarithmic functions, and second-order derivatives, readers can memorize the formula for calculating derivatives through a poem.

Quick view:

• What is derivative?
• Formula for derivative of a function at a point
• Derivatives of common functions
• Derivatives of sum, difference, product, quotient
• Derivative of composite function
• Derivatives of trigonometric functions
• Derivative of exponential function
• Derivative of logarithmic function
• Second derivative
• Tips to remember derivative formula

What is derivative?

According to Math 11, volume 2, Connecting knowledge and life series, the derivative of a function is one of the important concepts of mathematics. The derivative represents the rate of change of a function at a point or an interval.

Formula for derivative of a function at a point

The derivative of a function at a point tells how much the function changes at that point.

Derivatives of common functions

These are the simplest forms of power functions - the basis for calculating derivatives for more complex functions later.

Derivatives of sum, difference, product, quotient

Derivatives of sums, differences, products, and quotients are important rules that help us to calculate derivatives of complex expressions from simple functions. Instead of having to prove the definition of limits again, we can simply apply these rule formulas to simplify the operation.

Specifically, the derivative of the sum or difference is equal to the sum or difference of the derivatives; the derivative of the product follows the rule "derivative first, then multiplication, addition first, then multiplication of the derivative"; and the derivative of the quotient follows the rule "numerator of derivative multiplied by denominator, subtract numerator multiplied by denominator of derivative, divide by square of denominator". These formulas will be presented clearly below, with illustrative examples, so that students can easily remember and apply them to exercises.

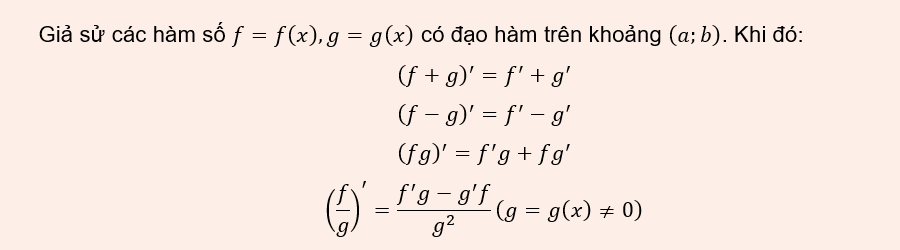
Derivative of composite function

The derivative of a composite function is used when the function is made up of several nested layers of functions. Applying the chain rule, the derivative of a composite function is equal to the derivative of the outer function, multiplied by the derivative of the inner function.

Derivatives of trigonometric functions

The derivatives of trigonometric functions help us know the rate of change of functions such as sin(x), cos(x) or tan(x) when the value of x changes.

Just by mastering the derivatives of sin(x) and cos(x), we can deduce the derivatives of other trigonometric functions, because they can all be expressed based on sin and cos (using the quotient rule).

In the following section, we will prove the derivative formula of sin(x) and cos(x). From there, we can calculate derivatives for other trigonometric functions as well as extend to inverse trigonometric functions and some other special formulas.

Derivative of exponential function

The derivative of an exponential function tells us the rate of change of functions of the form a ^x (with a>0,a≠1) or especially e ^x . Among them, e ^x is considered the most important exponential function because its derivative is equal to itself.

Derivative of logarithmic function

The derivative of a logarithmic function tells the rate of change of functions of the form log _⁡a (x) (with a>0, a≠1), the most important of which is ln⁡(x) - the natural logarithm with base e.

Knowing the derivative formula of ln⁡(x), we can easily deduce the derivative of log _⁡a (x) using the base change formula.

Second derivative

The second derivative is the derivative of the first derivative, that is, we take the derivative of a function twice in a row. If the first derivative tells us the rate of change of the function, then the second derivative tells us the rate of change of that same rate.

In geometry, the second derivative helps determine the curvature/concavity of a graph. In physics, if a function represents distance over time, the first derivative is the velocity, and the second derivative is the acceleration.

Tips to remember derivative formula

- Learn formulas in groups instead of separately.

- Save the formula table so you can apply it immediately when you forget.

- Learn derivatives through poems:

One hundred years in this world

Lazy to learn derivatives is to be absent-minded.

X with power n

We take the derivative to the first n power.

Then the exponent above

We subtract 1 right away.

Derivative of square root x my friend

With love, my friend, don't forget it.

The numerator is the integer 1.

Sample 2 square root x written together for quickness.

Derivative of the product of two brothers

I will teach you first, save you for later.

Then add a plus sign for quickness

Keep the front brother, the back brother derivative.

If you love, no matter how difficult it is, you will accept it.

The derivative and the denominator remain the same.

Don't forget the minus sign.

The origin of the universe and the mother's path follow closely behind.

Where does the sample square go?

I brought it down to quickly learn the lesson.

The derivative of sine is really talented.

It turns out cos is never wrong.

The derivative of a dream

Subtract sin to leave you alone.

Diligence makes up for intelligence

A division by cosine is the tangent derivative.

Only by studying hard can one be proud.

Although the funeral is difficult, it still has its derivatives.

Subtract 1 and remember to do it.

Be a normal person, don't be too playful.

E hat x is so strange

Its derivative, we keep the same.

We leave the exponential function alone.

The base number ran right after.

Nepe x derivative quickly

It's 1 divided by x, not that difficult.

Is logarithm x different?

Don't forget our base number.

(Collect)

Source: https://vietnamnet.vn/dao-ham-la-gi-cac-cong-thuc-dao-ham-chi-tiet-2452539.html