Formula for calculating the area of ​​a rectangle

To calculate the area of ​​a rectangle, in addition to multiplying the length by the width, it is also possible to calculate when knowing one side and adding the diagonal or perimeter.

Quick view:

• What is a rectangle?
• Formula for calculating the area of ​​a rectangle
• Formula for calculating the area of ​​a rectangle when knowing 1 side and diagonal
• Formula for calculating the area of ​​a rectangle when knowing the perimeter
• Signs to recognize a rectangle?
• Is a rectangle a parallelogram?
• Is a rectangle an isosceles trapezoid?

What is a rectangle?

According to Lesson 13, Math 8 (Volume 1) of the textbook series "Connecting knowledge with life" by Vietnam Education Publishing House, the definition of a Rectangle is a quadrilateral with 4 right angles.

The properties of a rectangle are that it has 2 parallel opposite sides, 2 equal opposite sides, 2 equal opposite angles, 2 equal diagonals and intersects at the midpoint of each line.

Formula for calculating the area of ​​a rectangle

In lesson 52, Math book 3 (Volume 2) of the textbook series "Connecting knowledge with life" by Vietnam Education Publishing House, the formula for calculating the area of ​​a rectangle is length multiplied by width (same unit of measurement).

S = axb

In there:

S: Area of ​​rectangle

a: Length of the rectangle

b: Width of the rectangle

For example: A rectangular wooden board has a width of 5cm and a length of 15cm. Calculate the area of ​​that wooden board.

Answer: The area of ​​the wooden board is: S = 5 x 15 = 75 (cm ² )

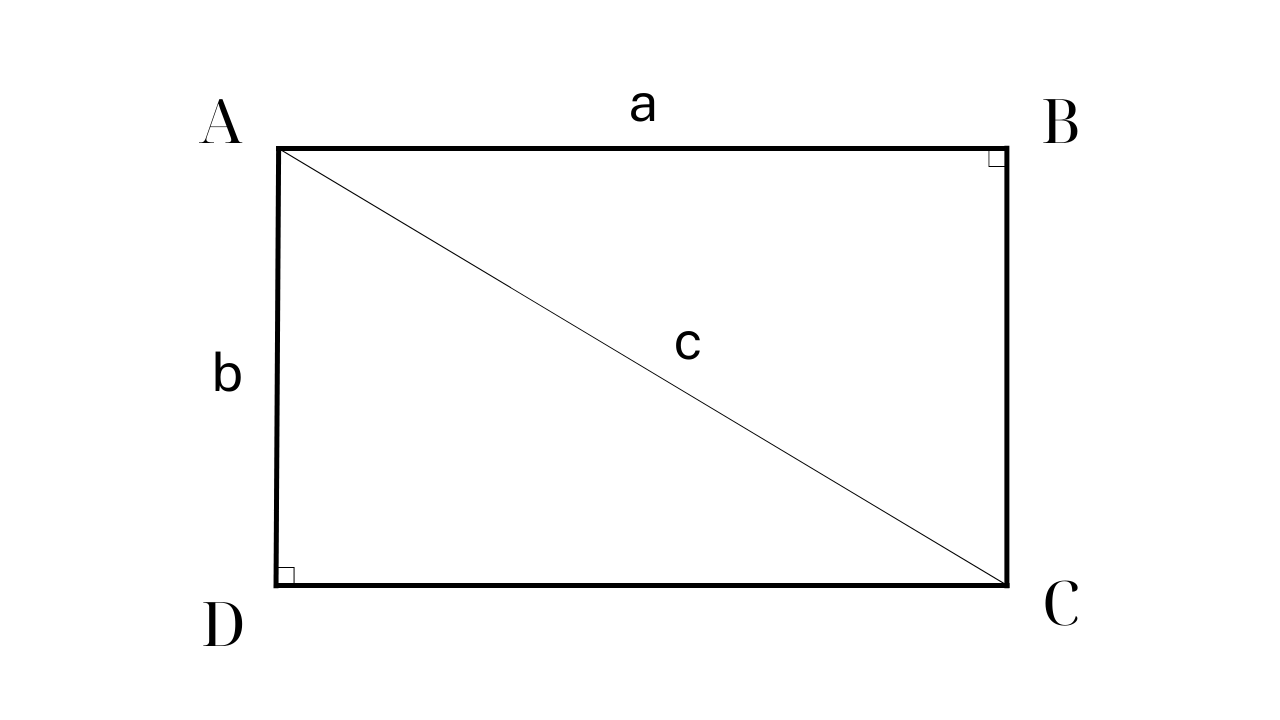
Formula for calculating the area of ​​a rectangle when knowing 1 side and diagonal

To calculate the area of ​​a rectangle when knowing the diagonal and one side, it is necessary to combine the Pythagorean theorem with the basic area formula.

Step 1: Apply the Pythagorean theorem in a right triangle to calculate the length of the remaining side.

Step 2: Apply the formula to calculate the area of ​​a rectangle: S = axb

For example: A rectangle ABCD has AD = 60cm, diagonal AC is 100cm. Calculate the area of ​​ABCD.

Answer:

Step 1: Find the remaining side of rectangle ABCD using the Pythagorean theorem in a right triangle.

Accordingly: AC ² =AB ² +AD ² => AB ² = AC ² - AD ² = 10000 - 3600 = 6400 => AB = 80 (cm)

Step 2: Area ABCD = AB x AD = 60 x 80 = 4800 (cm ² )

Formula for calculating the area of ​​a rectangle when knowing the perimeter

To calculate the area of ​​a rectangle when knowing the perimeter, you must combine the perimeter formula and the basic area formula.

Step 1: From the formula for calculating the perimeter of a rectangle is P = (a+b) x 2 with P is the perimeter, a is the length, b is the width of the rectangle, we have a = (P/2) - b or b = (P/2) - a

Step 2: After finding a or b, apply the formula to calculate the area of ​​a rectangle: S = axb

Signs to recognize a rectangle?

According to Lesson 13, Math 8 (Volume 1) Textbook series "Connecting knowledge with life" by Vietnam Education Publishing House, the signs to recognize a rectangle are:

- A quadrilateral has 3 right angles (based on the definition)

- Parallelogram has 1 right angle

- A parallelogram has two equal diagonals.

- An isosceles trapezoid has one right angle.

Is a rectangle a parallelogram?

According to Lesson 13, Math 8 (Volume 1) Textbook series "Connecting knowledge with life" by Vietnam Education Publishing House, a rectangle has all the properties of a parallelogram. Therefore, a rectangle is a special parallelogram.

Is a rectangle an isosceles trapezoid?

Lesson 13, Math 8 (Volume 1) Textbook series "Connecting knowledge with life" by Vietnam Education Publishing House, rectangle has all the properties of an isosceles trapezoid. Therefore, a rectangle is a special form of isosceles trapezoid.

(Synthetic)

Source: https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-chu-nhat-2445253.html