In everyday life, marshmallows are just a snack, weighing a few grams, made from gelatin, sugar and flavoring. But modern physics teaches us that energy depends not only on mass but also on Albert Einstein's famous formula: E=mc².
At the speed of light, any object with mass would become a giant energy bomb. And if a marshmallow traveling at that speed were to hit Earth, the consequences would be no small matter.
First, let's get a basic limit out of the way: according to special relativity, no object with mass can ever reach the speed of light (c). As the speed gets closer to c, the energy required to accelerate increases, until it reaches infinity. In other words, the marshmallow can't actually reach c.
However, for the sake of a hypothetical scenario, let's ignore this limitation and just consider it from a theoretical perspective, and imagine that the candy is traveling at or very close to the speed of light.
Suppose a marshmallow weighs 5 grams, that is 0.005 kg. The corresponding energy if that mass were completely converted according to the formula E=mc² would be:
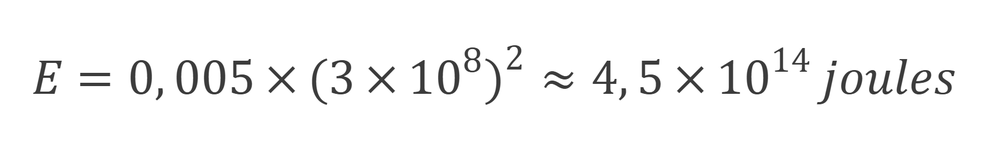
Interestingly, when compared to historical events, this figure is not far-fetched. The 1908 Tunguska event, when a small meteor exploded in the sky over Siberia, releasing the equivalent of 10-15 megatons of TNT, felling tens of millions of trees over an area of 2,000 km².
With a 100 kiloton TNT marshmallow, the immediate blast zone would be smaller than Tunguska, but still enough to obliterate a large city. The heat generated would incinerate everything within a few kilometers, while the shockwave would spread out for dozens of kilometers, destroying structures and causing massive casualties.
Not only that, when the marshmallow hits the atmosphere at the speed of light, the interaction will be extremely violent. The air in front of it will be compressed to the point of forming plasma, emitting a bright light and terrible heat.
This tiny object would turn into a super-velocity meteor, but instead of melting and burning up like a normal meteor, it would release its energy as soon as it hit the ground. A giant impact crater could be created, accompanied by a column of fire and a cloud of dust rising high into the stratosphere.

Illustration of a marshmallow falling to Earth at the speed of light (Photo: Whatifshow).
Even with just a few nuclear bombs, the local impact was enough to cause a small “artificial winter.” The dust from the impact could have blocked out the sun for weeks, causing localized temperature drops and crop failures.
If the scenario occurs in a densely populated area or near an industrial park, the consequences will be many times more severe due to the chain effect of fire, explosion and pollution.
From another perspective, this scenario also emphasizes the contrast between the innocent image of the marshmallow and the terrifying energy levels hidden in the physics formula.
A seemingly harmless object, associated with childhood and sweet joy, becomes a source of destruction simply because of a change in velocity. It reminds us that, in the physical world , everything has a hidden side that goes far beyond human intuition.
Of course, this whole scenario is hypothetical. In reality, accelerating an object with mass to the speed of light is impossible.
Even particles in large accelerators like the Large Hadron Collider (LHC) at CERN only travel at 99.999999% the speed of light, and they have masses that are infinitesimally small compared to a piece of candy. This further demonstrates the absurdity of the assumption, but also gives us a better idea of the energy scales that physics can reveal.
When you think about this scenario, you can see it as a kind of “physicalization” of the imagination: a small piece of candy can become a symbol of the hidden power of the universe. It shows that, in the world of science , seemingly small and funny things sometimes open up profound thoughts about the fragility of life on Earth.
Source: https://dantri.com.vn/khoa-hoc/dieu-gi-xay-ra-neu-mot-vien-keo-deo-roi-xuong-trai-dat-voi-toc-do-anh-sang-20250915232717466.htm









































































































Comment (0)